Karush Kuhn Tucker Proximity Measure (KKTPM)#
In 2016, Deb and Abouhawwash proposed Karush Kuhn Tucker Proximity Measure (KKTPM) [57], a metric that can measure how close a point is from being “an optimum”. The smaller the metric, the closer the point. This does not require the Pareto front to be known, but the gradient information needs to be approximated. Their metric applies to both single objective and multi-objective optimization problems.
In a single objective problem, the metric shows how close a point is from being a “local optimum”, while in multi-objective problems, the metric shows how close a point is from being a “local Pareto point”. Exact calculations of KKTPM for each point requires solving a whole optimization problem, which is extremely time-consuming. To avoid this problem, the authors of the original work again proposed several approximations to the true KKTPM, namely Direct KKTPM, Projected KKTPM, Adjusted KKTPM, and Approximate KKTPM. Approximate KKTPM is simply the average of the former three and is what we call simply “KKTPM”. Moreover, they were able to show that Approximate KKTPM is reliable and can be used in place of the exact one [58].
Let us now see how to use pymoo to calculate the KKTPM for a point:
[1]:
from pymoo.constraints.from_bounds import ConstraintsFromBounds
from pymoo.gradient.automatic import AutomaticDifferentiation
from pymoo.problems import get_problem
problem = AutomaticDifferentiation(ConstraintsFromBounds(get_problem("zdt1", n_var=30)))
For instance, the code below calculates the KKTPM metric for randomly sampled points for the given example:
[2]:
from pymoo.indicators.kktpm import KKTPM
from pymoo.operators.sampling.rnd import FloatRandomSampling
X = FloatRandomSampling().do(problem, 100).get("X")
kktpm = KKTPM().calc(X, problem)
Moreover, a whole run of a genetic algorithm can be analyzed by storing each generation’s history and then calculating the KKTPM metric for each of the points:
[3]:
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
from pymoo.core.evaluator import Evaluator
algorithm = NSGA2(pop_size=100, eliminate_duplicates=True)
# make sure each evaluation also has the derivatives - necessary for KKTPM
evaluator = Evaluator(evaluate_values_of=["F", "G", "dF", "dG"])
res = minimize(problem,
algorithm,
('n_gen', 100),
evaluator=evaluator,
seed=1,
save_history=True,
verbose=False)
[4]:
import pandas as pd
import numpy as np
# Collect KKTPM data for each generation
data = []
for algorithm in res.history:
if algorithm.n_gen % 5 == 0:
X = algorithm.pop.get("X")
kktpm = KKTPM().calc(X, problem)
# Add each individual's KKTPM value with generation info
for i, value in enumerate(kktpm):
data.append({
'generation': algorithm.n_gen,
'individual': i,
'kktpm': value
})
# Create DataFrame
df = pd.DataFrame(data)
df
[4]:
| generation | individual | kktpm | |
|---|---|---|---|
| 0 | 5 | 0 | 0.578128 |
| 1 | 5 | 1 | 0.556041 |
| 2 | 5 | 2 | 0.481507 |
| 3 | 5 | 3 | 0.638571 |
| 4 | 5 | 4 | 0.552443 |
| ... | ... | ... | ... |
| 1995 | 100 | 95 | 0.006646 |
| 1996 | 100 | 96 | 0.007908 |
| 1997 | 100 | 97 | 0.011097 |
| 1998 | 100 | 98 | 0.007232 |
| 1999 | 100 | 99 | 0.009157 |
2000 rows × 3 columns
[5]:
# Get summary statistics for each generation
stats_by_gen = df.groupby('generation')['kktpm'].describe()
stats_by_gen
[5]:
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| generation | ||||||||
| 5 | 100.0 | 0.606367 | 0.102607 | 0.413505 | 0.531672 | 0.601515 | 0.691302 | 0.823210 |
| 10 | 100.0 | 0.437565 | 0.100178 | 0.256413 | 0.352657 | 0.426188 | 0.525569 | 0.625640 |
| 15 | 100.0 | 0.327390 | 0.084982 | 0.199976 | 0.256976 | 0.313050 | 0.392336 | 0.495058 |
| 20 | 100.0 | 0.234454 | 0.073420 | 0.109959 | 0.181489 | 0.200261 | 0.294889 | 0.402596 |
| 25 | 100.0 | 0.184949 | 0.048054 | 0.077966 | 0.152082 | 0.166390 | 0.227511 | 0.295211 |
| 30 | 100.0 | 0.157165 | 0.041126 | 0.063416 | 0.128238 | 0.143977 | 0.190136 | 0.279304 |
| 35 | 100.0 | 0.122228 | 0.033381 | 0.028348 | 0.103134 | 0.112931 | 0.141745 | 0.190694 |
| 40 | 100.0 | 0.100814 | 0.026641 | 0.020273 | 0.083457 | 0.095660 | 0.112486 | 0.166559 |
| 45 | 100.0 | 0.078313 | 0.020058 | 0.019823 | 0.068038 | 0.074447 | 0.086282 | 0.134496 |
| 50 | 100.0 | 0.062054 | 0.013506 | 0.015916 | 0.055734 | 0.059743 | 0.068355 | 0.113593 |
| 55 | 100.0 | 0.047471 | 0.010750 | 0.016135 | 0.039670 | 0.047031 | 0.054423 | 0.071587 |
| 60 | 100.0 | 0.034896 | 0.007247 | 0.012692 | 0.030444 | 0.033539 | 0.038914 | 0.057769 |
| 65 | 100.0 | 0.035714 | 0.039961 | 0.013633 | 0.023666 | 0.029073 | 0.034778 | 0.258761 |
| 70 | 100.0 | 0.022869 | 0.005775 | 0.011882 | 0.018193 | 0.022407 | 0.025962 | 0.039261 |
| 75 | 100.0 | 0.017109 | 0.003856 | 0.009919 | 0.014264 | 0.016124 | 0.019667 | 0.031376 |
| 80 | 100.0 | 0.016684 | 0.024352 | 0.008281 | 0.012165 | 0.013918 | 0.016429 | 0.256016 |
| 85 | 100.0 | 0.012111 | 0.002707 | 0.007561 | 0.010196 | 0.011751 | 0.013273 | 0.021814 |
| 90 | 100.0 | 0.010202 | 0.002392 | 0.005750 | 0.008470 | 0.009991 | 0.011494 | 0.018209 |
| 95 | 100.0 | 0.009075 | 0.002409 | 0.005070 | 0.007201 | 0.008927 | 0.010152 | 0.019328 |
| 100 | 100.0 | 0.007976 | 0.001966 | 0.004577 | 0.006687 | 0.007807 | 0.008869 | 0.014139 |
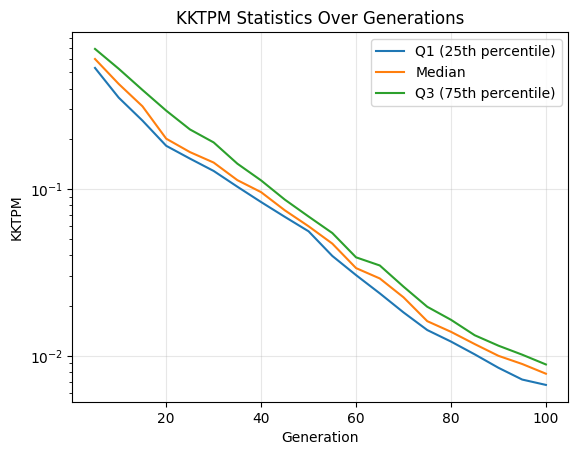
[6]:
import matplotlib.pyplot as plt
# Plot the quartiles and median over generations
generations = stats_by_gen.index
plt.plot(generations, stats_by_gen['25%'], label="Q1 (25th percentile)")
plt.plot(generations, stats_by_gen['50%'], label="Median")
plt.plot(generations, stats_by_gen['75%'], label="Q3 (75th percentile)")
plt.yscale("log")
plt.xlabel("Generation")
plt.ylabel("KKTPM")
plt.title("KKTPM Statistics Over Generations")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()